Библиотека численных методов на языке Fortran 90. Вычисление минимума функции.

Автор cайта:
Владимир
Потемкин
fortran-90@yandex.ru

Вычисление минимума функции

FMIN. Вычисление минимума функции f(x) в заданном интервале [a,b].

FM25. Вычисление минимума f(x1,x2,...,xn) методом Хука-Дживса.

FM28. Вычисление минимума f(x1,x2,...,xn) методом Нелдера-Мида.

FM31. Вычисление минимума f(x1,x2,...,xn) методом Давидона-Флетчера-Пауэлла.

FM34. Вычисление минимума f(x1,x2,...,xn) методом Флетчера-Ривса.

FMIN

Программа Fmin вычисляет минимум функции f(x) в заданном интервале [a,b] комбинацией методов золотого сечения и параболической интерполяции.
Подробное описание программы "FMIN" можно найти в книге [Б3].

Вызов программы

Fmin(Fun, AX, BX, Eps)

Параметры программы

Fun, AX, BX, Eps - входные параметры;
Real Fmin - возвращаемое значение;
Real Fun(Real X) - исследуемая функция;
Real AX, BX - границы интервала, AX<BX;
Real Eps - погрешность решения.

Пример

!Поиск минимума функции одной переменной
program TestFMIN
    use NML
    implicit none
    integer:: Count=0
    real:: A, B, R, FR, Eps
    data A/-1.0/, B/1.0/, Eps/1.0E-5/
    !begin
      R=FMIN(Fun, A, B, Eps)
      FR=Fun(R); Count=Count-1
      print 10, R, Count
      print 11, FR
10    format(/'Minimum =',F11.7,'   Count =',I3)
11    format('The value of the function'/'at the point of minimum ',F12.7)
    !end

    contains

    real function Fun(x)
    real, intent(in):: x
      Fun=x*x*x*x+5.0
      Count=Count+1
      return
    end function Fun

end program TestFMIN

Minimum =  0.0131775   Count = 24
The value of the function
at the point of minimum    5.0000000

Вернуться к оглавлению Скачать FMIN

FM25

Программа FM25 вычисляет минимум функции нескольких переменных f(x₁,x₂,...,x_n) методом Хука-Дживса.
В методе Хука-Дживса используются только значения самой функции, без использований частных производных (градиента) функции.

Для начала вычислений нужно указать начальное приближение (базисную точку) b₁ с координатами b₀, b₁,…, b_n и начальный шаг h_i (i=1,…,n) по каждой координате. Когда начальные параметры заданы, вычисляем значение функции в базисной точке b₁ и в точке, смещённой по оси x₁ на шаг h₁. Если значение функции в смещённой точке меньше, чем в базисной, то принимаем смещённую точку за новую базисную. В противном случае (функция не стала меньше) делаем смещение в противоположную сторону на шаг -h₁ и вычисляем функцию в этой точке. Если значение функции меньше, переносим базисную точку в эту сторону, иначе оставляем её на прежнем месте. Далее аналогично поступаем с координатой x₂ и со всеми остальными до x_n.

В результате такого исследования наша базисная точка могла сместиться на новое место по n-мерной поверхности, но могла и остаться на месте. Если смещения не произошло, уменьшаем величину шага по каждой координате и повторяем исследование вокруг этой же точки с меньшим шагом. Практика показывает, что эффективно уменьшать шаг в 10 раз.

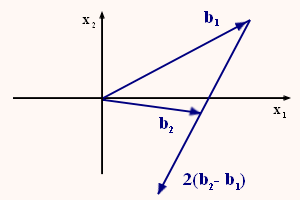
Если базисная точка сместилась, далее выполняем поиск по образцу. Образец (т.е. новая базисная точка) выбирается на линии, соединяющей начальную и смещённую базисные точки и в направлении от b₁ к b₂. Расстояние увеличиваем в два раза. В векторной форме это будет иметь вид:
b₃ = b₁ + 2(b₂ - b₁).
Или в общем случае:
b_i+2 = b_i + 2(b_i+1 - b_i),
где b_i+2 новая базисная точка (образец), вокруг которой снова будем выполнять исследование.

sample

Этот процесс продолжается, пока шаг h не станет меньше значения h < µx_min+ε, где x_min – минимальная из координат последней базисной точки, µ – квадратный корень из машинного эпсилон, ε – желаемая точность результата, которая задаётся при вызове.
Было бы полезно указывать свою величину шага для каждой координаты точки b_i, но в данной программе, ради упрощения, шаг одинаков по всем координатам.

[Б12]. Метод Хука-Дживса

Вызов программы

call FM25(Fun, X, H, Eps)

Параметры программы

Fun, H, Eps - входные параметры;
Real X[N] - входной и выходной параметр;
Real Fun(Real X(N)) - исследуемая функция;
Real H - начальный шаг;
Real Eps - относительная точность;
Integer N - количество переменных.

Пример

!Поиск минимума функции нескольких переменных
!f(x1,x2,...,xn) методом Хука-Дживса
program TestFM25
    use NML
    implicit none
    integer, parameter:: N=3
    real X(N), H, Eps
    data X/4.0, -2.0, 3.0/, H/1.0/, Eps/1.0E-6/
    integer:: Count=0
    integer i
    real FR
    !begin
      call FM25(Fun, X, H, Eps)
      FR=Fun(X); Count=Count-1
      print 10, (X(i), i=1, N)
      print 11, FR
      print 12, Count
10    format(/'The point of a minimum'/<N>(4X,F8.5))
11    format('The value of the function'/'at the point of minimum ',F13.7)
12    format(/'The number of function evaluations ',I3)
    !end

    contains

    real function Fun(X)
    real, intent(in):: x(:)
      Fun=(X(1)-2.0)**2+(X(2)-5.0)**2+(X(3)+2.0)**4
      Count=Count+1
      return
    end function Fun

end program TestFM25

!=========== Вывод программы
 The minimum
  X[1]= 2.000000  X[2]= 5.000000  X[3]=-2.000000
 The minimum of the function is  0.0000000E+00
 The number of iterations          30

The point of a minimum
     2.00000     5.00000    -2.00000
The value of the function
at the point of minimum     0.0000000

The number of function evaluations  91

Вернуться к оглавлению Скачать FM25

FM28

Программа FM28 вычисляет минимум функции нескольких переменных f(x₁,x₂,...,x_n) методом Нелдера-Мида.
В методе Нелдера-Мида используются только значения самой функции, без использований частных производных (градиента) функции.

Регулярным симплексом в n-мерном пространстве называется множество (n+1) равноудалённых точек. Так, для двухмерного пространства это будет равнобедренный треугольник, для трёхмерного – правильный тетраэдр. Идея метода заключается в следующем. Исходя из некоторой начальной точки и начального шага строится (n+1)-мерный симплекс, произвольной формы, не обязательно регулярный. В вершинах симплекса вычисляются значения функции f₁= f(x₁), f₂= f(x₂), …, f_n= f(x_n). Находим наименьшее значение функции f_l, наибольшее значение f_h, значение, предшествующее наибольшему f_g и соответствующие им точки x_l, x_h, x_g. Выбираем числа α, β, γ (альфа, бета, гамма) как коэффициенты для операций отражения, сжатия, растяжения соответственно. Дальнейшие наши действия представлены в виде следующего алгоритма.

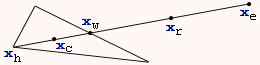
schema

1. Вычисляем центр тяжести x_w как среднее арифметическое всех точек, за исключением точки x_h.

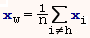
summa

2. Выполняем отражение. Точку x_r вычисляем как отражение точки x_h относительно точки x_w.
x_r = - αx_h + (1+α)x_w
Вычисляем f_r= f(x_r) и в зависимости от значения f_r выбираем один из вариантов:
─ Если f_r < f_l, то мы двигаемся в правильном направлении и выполняем растяжение. Продвигаем x_r далее на расстояние γ. x_e = γx_r + (1 – γ)x_w и вычисляем f_e= f(x_e). Если f_e < f_l то полагаем x_h=x_e, иначе (f_e > f_l) мы продвинулись слишком далеко и x_h= x_r. Переходим к пункту 5.
─ Если f_r находится между f_l и f_g (f_l < f_r < f_g) полагаем x_h= x_r. Переходим к пункту 5.
─ Если f_r находится между f_g и f_h (f_g < f_r < f_h) то меняем местами точки x_r и x_h. Переходим к пункту 3.

3. f_r > f_h. Выполняем сжатие. Строим точку x_c = βx_h + (1 - β)x_w и вычисляем f_c= f(x_c). В зависимости от значения f_c выбираем один из вариантов:
─ Если f_c < f_h то присваиваем x_h= x_c и идём к пункту 5.
─ Если f_c > f_h то это означает, что исходные точки были самыми удачными. Переходим к пункту 4.

4. Совершаем сжатие симплекса. Делим пополам расстояния от каждой точки симплекса до точки с наименьшим значением функции x_l, т.е. все x_i заменяются на x_i + ½(x_i - x_l), i≠l

5. Завершающий шаг – проверка критерия завершения. Если критерий завершения не выполняется, то совершаем нужные переобозначения точек и значений функции в этих точках и возвращаемся к пункту 1.

В качестве критерия завершения используем среднеквадратичное отклонение значений функции в точках симплекса σ от их среднеарифметического значения.
Вычисления прекращаем, если σ окажется меньше заданного значения ε.

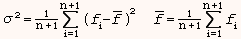
sigma

Коэффициенты для операций отражения, сжатия, растяжения Недлер и Мид рекомендуют брать α=1, β=0.5, γ=2.

[Б12]. Метод Нелдера-Мида

Вызов программы

call FM28(Fun, X, H, Alpha, Beta, Gamma, Eps)

Параметры программы

Fun, H, Alpha, Beta, Gamma, Eps - входные параметры;
Real X[N] - входной и выходной параметр;
Real Fun(Real X(N)) - исследуемая функция;
Real H - начальный шаг;
Real Alpha, Beta, Gamma - коэффициенты отражения, сжатия и растяжения;
Real Eps - абсолютная точность;
Integer N - количество переменных.

Пример

!Поиск минимума функции нескольких переменных
!f(x1,x2,...,xn) симплексным методом Нелдера-Мида
program TestFM28
    use NML
    implicit none
    integer, parameter:: N=2
    real X(N), H, Eps
    data X/1.5, 2.0/, H/0.5/, Eps/1.0E-5/
    real Alpha, Beta, Gamma  !коэффициенты сжатия
    data Alpha/1.0/, Beta/0.5/, Gamma/2.0/
    integer:: Count=0
    integer i
    real FR
    !begin
      call FM28(Fun, X, H, Alpha, Beta, Gamma, Eps)
      FR=Fun(X); Count=Count-1
      print 10, (X(i), i=1, N)
      print 11, FR
      print 12, Count
10    format(/'The point of a minimum'/<N>(4X,F8.5))
11    format('The value of the function'/'at the point of minimum ',F13.7)
12    format(/'The number of function evaluations ',I3)
    !end

    contains

    real function Fun(X)
    real, intent(in):: x(:)
      Fun=100.0*(X(2)-X(1)*X(1))**2+(1.0-X(1))**2
      Count=Count+1
      return
    end function Fun

end program TestFM28

!=========== Вывод программы
 The minimum
  X[1]= 1.000634  X[2]= 1.001357
 The minimum of the function is  1.1944242E-06
 The number of iterations          37

The point of a minimum
     1.00063     1.00136
The value of the function
at the point of minimum     0.0000012

The number of function evaluations 108

Вернуться к оглавлению Скачать FM28

FM31

Программа FM31 вычисляет минимум функции нескольких переменных f(x) = f(x₁,x₂,...,x_n) методом Дэвидона-Флетчера-Пауэлла.
В методе Давидона-Флетчера-Пауэлла в ходе вычислений используются значения самой функции и её частных производных (градиента).

Любую функцию f(x) в случае её непрерывности и непрерывности её производных можно разложить в ряд Тейлора в окрестности точки x₀:
f(x - x₀) - f(x₀) = (x - x₀)^Tg(x₀) + ½(x - x₀)^TG(x₀)(x - x₀) + ...
где g(x₀) = ∇f(x₀) - градиент функции, G(x₀) - её матрица Якоби (матрица Гессе), градиент и матрица Якоби вычислены в точке x₀.

В качестве разумной аппроксимации функции f(x) в окрестности точки минимума можно принять квадратичную функцию φ(x):
φ(x) = f(x₀) + (x - x₀)^T∇(x₀) + ½(x - x₀)^TG(x₀)(x - x₀)
Если её минимум находится в точке x_m, то
∇φ(x_m) = ∇f(x₀) + G(x₀)(x_m – x₀) = 0
откуда
x_m = x₀ – G^-1(x₀)∇f(x₀) = x₀ – G^-1(x₀)g(x₀)
Таким образом, для нахождения точки минимума можно предложить следующий итерационный процесс:
x_i+1 = x_i – G^-1(x_i)g(x_i)
или, в более общем виде
x_i+1 = x_i – λ_iG^-1(x_i)g(x_i)
где длина шага λ_i определяется одномерной минимизацией в направлении G^-1(x_i)g(x_i)

Метод Ньютона-Рафсона поиска минимума функции f(x) основан на последнем уравнении и требует вычисления и обращения матрицы Якоби на каждом шаге (т.е. при каждой итерации). Этот процесс весьма трудоёмкий в случае, если количество переменных n больше двух. В методе Давидона-Флетчера-Пауэлла на i-ом шаге вычисляется одномерный минимум в направлении –H_ig_i = -H_ig(x_i), где H_i – симметричная положительно-определённая матрица, которая в конце вычислений становится равной -G^-1(x_m). Т.е. в этом методе удаётся избежать как вычисления матрицы Якоби, так и её обращения.

Для начала вычислений выбираем точку x₀, матрицу H полагаем равной единичной матрице. Далее выполняем следующий итерационный процесс.
1. Выбираем направление поиска d_i = - H_ig_i
2. Находим коэффициенты λ_i, минимизирующие функцию f(x_i + λ_id_i), что эквивалентно одномерному поиску минимума вдоль прямой x_i + λ_id_i
3. Полагаем v_i = λ_id_i и x_i+1 = x_i + v_i
4. Находим f(x_i+1) и g_i+1. Если величины |g_i+1| и |v_i| достаточно малы, то завершаем процесс.
5. Полагаем u_i = g_i+1 – g_i
6. Обновляем матрицу H:
H_i+1 = H_i + A_i + B_i
где A_i = v_iv_i^T/(v_i^Tu_i), B_i = -H_iu_iu_i^TH_i/(u_i^TH_iu_i)
7. Увеличиваем i на 1 и возвращаемся к пункту 1.

Для минимизации функции ψ(x_i + λd_i) по параметру λ (т.е. одномерного поиска минимума f(x) в направлении x_i + λd_i) применяется кубическая интерполяция по значениям функции и её производной в точках p = x_i и q = x_i + λd_i

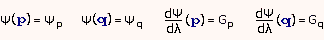
Минимум достигается в точке r и равен [Б12]

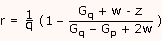
где z = 3(ψ_p – ψ_q)/q + G_p + G_p и w = (z² – G_pG_p)^½

[Б12]. Метод Давидона-Флетчера-Пауэлла
Программа требует долненительного тестирования для устранения возможных неточностей кода

Вызов программы

call FM31(Fun, Grad, X, Eps, Delta)

Параметры программы

Fun, Grad, X, Eps, Delta - входные параметры;
Real X[N] - входной и выходной параметр;
Real Fun(Real X[N]) - исследуемая функция;
Real Grad(Real X[N], Real G[N]) - функция вычисления градиента;
Real Eps - абсолютная точность вычисления градиента;
Real Delta - абсолютная точность вычисления аргумента;
Integer N - количество переменных.

Пример

!Поиск минимума функции нескольких переменных
!f(x1,x2,...,xn) методом Давидона-Флетчера-Пауэлла
program TestFMIN
    use NML
    implicit none
    integer, parameter:: N=4
    real X(N), Eps, Delta
    data X/3.0, -1.0, 0.0, 1.0/, Eps/5.0E-5/, Delta/1.0E-5/
    integer:: Count=0
    integer i
    real FR
    !begin
      call FM31(Fun, Grad, X, Eps, Delta)
      FR=Fun(X); Count=Count-1
      print 10, (i, X(i), i=1, N)
      print 11, FR
      print 12, Count
10    format(/'The point of a minimum'/<N>(2X,'X[',I1,']=',F10.7))
11    format('The value of the function'/'at the point of minimum ',E14.7)
12    format(/'The number of function evaluations ',I3)
    !end

    contains

    real function Fun(X)
    real, intent(in):: x(:)
    real Z
      Z=(x(1)+10.0*x(2))**2+5.0*(x(3)-x(4))**2
      Z=Z+(x(2)-2.0*x(3))**4+10.0*(x(1)-x(4))**4
      Fun=Z
      Count=Count+1
      return
    end function Fun

    real function Grad(X, G)
    real, intent(in):: X(:)
    real:: G(:)
    real GG
    integer i, n
      n=size(X); GG=0.0
      G(1)=2.0*(X(1)+10.0*X(2))+40.0*(X(1)-X(4))**3
      G(2)=20.0*(X(1)+10.0*X(2))+4.0*(x(2)-2.0*x(3))**3
      G(3)=10.0*(X(3)-X(4))-8.0*(x(2)-2.0*x(3))**3
      G(4)=-10.0*(x(3)-x(4))-40.0*(X(1)-X(4))**3
      do i=1,n; GG=GG+G(i)*G(i); enddo
      Grad=sqrt(GG)
      return
    end function Grad

end program TestFMIN

!=========== Вывод программы
The point of a minimum
  X[1]= 0.0022939  X[2]=-0.0002294  X[3]= 0.0013408  X[4]= 0.0013402
The value of the function
at the point of minimum  0.8188328E-10

The number of function evaluations 129

Вернуться к оглавлению Скачать FM31

FM34

Программа FM34 вычисляет минимум функции нескольких переменных f(x) = f(x₁,x₂,...,x_n) методом Флетчера-Ривса

Направление градиента это направление, в котором функция возрастает наиболее быстро. Следовательно, в противоположное направление будет показывать наибольшее убывание функции. Возьмем произвольную точку x₀ и совершим перемещение из этой точки в направлении –∇f(x₀) на расстояние d. Выполним теперь одномерный поиск и найдём то расстояние d, на котором наша функция f(x) примет минимальное значение. Это будет следующая точка x₁ в приближении к минимуму функции f(x). Таким образом, можно построить итерационный процесс
x_i+1 = x_i – d_i∇f(x_i)
где di – параметр d (расстояние), на шаге i минимизирующий функцию
φ(d) = f(x_i – d_i∇f(x_i))
Мы получили метод наискорейшего градиентного спуска.

На практике для вычислений этот метод применяется редко и не рекомендуется для использования. Связано это с тем, что направление наискорейшего спуска является лишь локальным свойством и поэтому программа на его основе требует частой смены направлений, что и приводит к невысокой эффективности вычислений. Более быстрый и эффективный метод может быть предложен на основе свойств квадратичных функций.

В окрестностях минимума разложение в ряд Тейлора любой функции можно аппроксимировать квадратичной функцией (если её вторые производные не равны нулю):
F(x) = a + x^Tb + ½x^TGx
где a – константа, b – постоянный вектор, G – симметричная положительно-определённая матрица. Минимум F(x) в точке x_m достигается при условии
∇F(x_m) = b + Gx_m = 0
откуда x_m = - G^-1b

Два направления p и q в n-мерном пространстве называются сопряженными, если их скалярное произведение относительно симметричной положительно-определённой матрицы G (порядка n×n)
p^TGq = 0
В n-мерном пространстве n взаимно-сопряженных направлений являются линейно-независимыми и могут выступать в качестве базиса этого пространства. Можно показать [Б12], что если поиск минимума квадратичной функции F(x) производить по взаимно-сопряженным направлениям, то он будет найден не более чем через n шагов.

Алгоритм поиска можно составить так. В качестве первого направления из начальной точки x₀ возьмём направление наискорейшего спуска
d₁ = - ∇F(x₀) = - g₁
и найдём значение λ₁, минимизрующую функцию φ(λ) = f(x₁ + λd₁). Положим
x₂ = x₁ + λ₁d₁
и проведём минимизирующий поиск в направлении d₂, сопряжённом с d₁ и найдём
x₃ = x₂ + λ₂d₂
и т.д. до x_n. В случае квадратичной функции F(x) минимум должен быть найден. Данный метод применим и к произвольной функции, если поиск производится вблизи точки минимума, правда, в этом случае процесс может не завершиться на n-ом шаге. Флетчер и Ривс полагают, что в этой ситуации после построения всех сопряжённых направлений должен быть проведён рестарт и каждое n-ое направление поиска должно быть направлением наискорейшего спуска.

Для начала вычислений выбираем точку x₁. Далее выполняем следующий итерационный процесс.
1. Определяем направление наискорейшего спуска d_i = - g_i
2. Находим значение λ₁, минимизирующее функцию f(x_i + λd_i)
3. Полагаем x_i+1 = x_i + λ₁d_i
4. Если x+1_i точка минимума, то заканчиваем вычисления, иначе переходим к пункту 5.
5. Если i = n, то полагаем i = 1 и переходим к пункту 1, иначе к пункту 6.
6. Вычисляем k = |g_i+1|²/|g_i|²; полагаем d_i+1 = - kd_i
7. Увеличиваем i на 1 и возвращаемся к пункту 2.

Для вычисления минимума функции f(x_i + λd_i) применяем кубическую интерполяцию по значениям функции и её градиента в двух точках (см. FM31).

[Б12]. Метод Флетчера-Ривса
Программа требует долненительного тестирования для устранения возможных неточностей кода

Вызов программы

call FM34(Fun, Grad, X, Eps)

Параметры программы

Fun, Grad, X, Eps, Delta - входные параметры;
Real X[N] - входной и выходной параметр;
Real Fun(Real X[N]) - исследуемая функция;
Real Grad(Real X[N], Real G[N]) - функция вычисления градиента;
Real Eps - абсолютная точность вычисления аргумента;
Integer N - количество переменных.

Пример

!Поиск минимума функции нескольких переменных
!f(x1,x2,...,xn) методом Флетчера-Ривса
program TestFMIN
    use NML
    implicit none
    integer, parameter:: N=3
    real X(N), Eps
    data X/9.0, -7.0, 11.0/, Eps/5.0E-5/
    integer:: Count=0
    integer i
    real FR
    !begin
      call FM34(Fun, Grad, X, Eps)
      FR=Fun(X); Count=Count-1
      print 10, (i, X(i), i=1, N)
      print 11, FR
      print 12, Count
10    format(/'The point of a minimum'/<N>(2X,'X[',I1,']=',F9.6))
11    format('The value of the function'/'at the point of minimum ',F13.7)
12    format(/'The number of function evaluations ',I3)
    !end

    contains

    real function Fun(X)
    real, intent(in):: x(:)
    real Z
      Z=3.0*(X(1)-1.0)**2+2.0*(X(2)-2.0)**2+(X(3)-3.0)**2
      Fun=Z
      Count=Count+1
      return
    end function Fun

    real function Grad(X, G)
    real, intent(in):: X(:)
    real:: G(:)
    real GG
    integer i, n
      n=size(X); GG=0.0
      G(1)=6.0*(X(1)-1.0)
      G(2)=4.0*(X(2)-2.0)
      G(3)=2.0*(X(3)-3.0)
      do i=1,n; GG=GG+G(i)*G(i); enddo
      Grad=sqrt(GG)
      return
    end function Grad

end program TestFMIN

!=========== Вывод программы
The point of a minimum
  X[1]= 1.000000  X[2]= 2.000000  X[3]= 3.000000
The value of the function
at the point of minimum     0.0000000

The number of function evaluations   7

Вернуться к оглавлению Скачать FM34