PL10
Программа PL10 вычисляет значение функции y(x) в заданной точке x с помощью интерполяционного процесса Эйткена-Лагранжа.
Функция y(x) задана таблично массивами Xi и Yi, i=1, 2, ..., n. Массив Xi должен быть упорядочен в возрастающем порядке, т.е. для всех его элементов xi<xi+1. Максимальное число узлов m, используемых для интерполяции, задается при вызове программы.
Процесс интерполяции построен по итерационной схеме. В качестве первого приближения используется значение функции в ближайшем узле интерполяции. Для получения более точных приближений используются последовательно вычисляемые значения многочлена Лагранжа L(k)(x), степень которого возрастает на каждом шаге итерации:
![]()
где ω(k)(x) = (x-x1)(x-x2) ... (x-xk+1), k=1, 2, ..., n-1. Итерационный процесс продолжается до получения заданной точности интерполяции.
Вычисления проводятся по треугольной интерполяционной схеме Эйткена:
x1 y1
x2 y2 L12
x3 y3 L13 L123
x4 y4 L14 L124 L1234
. . . . . . . . . . . . . . . . . .
xm ym L1m L12m L123m ... L123...m
Каждый многочлен Лагранжа более высокой степени получается из двух предыдущих многочленов по рекуррентным формулам:
![]()
![]()
Элементы L12...k нисходящей диагонали этой схемы представляют собой интерполяционные многочлены Лагранжа L(k)(x) последовательно возрастающих степеней (k=2, ..., m).
Для определения значений многочлена L(k)(x) при росте k в вычислительный процесс вовлекаются все более удаленные от x узлы интерполяции. Поэтому значения xk и yk (k=1, 2, ..., m) предварительно упорядочиваются таким образом, чтобы модули разностей |xk - x| возрастали при росте индекса k:
|xk - x| ≤ |xk+1 - x|.
Вызов программы
CALL PL10(X, Y, XX, M, Eps, YY, Error)
Параметры программы
X, Y, XX, M, Eps - входные параметры;
YY, Error - выходные параметры;
Real X(1:N), Y(1:N) - массивы, содержащие значения аргумента и функции. Массив X должен быть упорядочен в возрастающем порядке;
Real XX - значение аргумента, в котором требуется вычислить значение функции, X[1] <= XX <= X[N];
Integer M - число узлов, которое разрешается использовать при интерполяции, 1 <= M <= N;
Real Eps - погрешность, с которой требуется вычислить значение функции;
Real YY - значение функции, вычисляемое программой;
Integer Error - индикатор ошибки, принимающий при выполнении программы одно из следующих значений:
Error=0 - заданная точность интерполяции достигнута, ошибок нет;
Error=1 - заданная точность не достигается или достигнутая точность не может быть проверена, т.к. мало значение M;
Error=2 - заданная точность не достигается из-за роста вычислительной погрешности или плохого поведения старших производных интерполируемой функции.
Пример
! Интерполяция функции многочленом Лагранжа
! по интерполяционной схеме Эйткена.
program TestPL10
use NML
implicit none
integer, parameter:: n=40
real:: X(n), Y(n), XX, YY, YE, Eps
integer:: M, Er
integer i
!begin
M=6
Eps=1.E-6
do i=1, n
X(i)=0.5*float(i-1)
Y(i)=exp(-X(i))*sin(X(i))
end do
XX=4.2
! YE - точное значение по формуле
YE=exp(-XX)*sin(XX)
! YY - значение, полученное интерполяцией
call PL10(X, Y, XX, M, Eps, YY, Er)
print 10, Er
print 11, XX, YE, YY
10 format(/' Error =',I2/)
11 format(' X = ',F6.2,' YE =',F11.6,' YY =',F11.6/)
end program TestPL10
────────────
Error = 1
X = 4.20 YE = -0.013070 YY = -0.013074
PL12
Программа PL12 вычисляет значение функции y(x) в заданной точке x с помощью интерполяционного процесса Эйткена-Эрмита.
Функция y(x) задана таблично массивами Xi и Yi, i=1, 2, ..., n. Массив Xi должен быть упорядочен в возрастающем порядке, т.е. для всех его элементов xi<xi+1. Максимальное число узлов m, используемых для интерполяции, задается при вызове программы.
Процесс интерполяции построен по итерационной схеме. В качестве первого приближения используется интерполяционный многочлен Эрмита первой степени. На каждой новой итерации степень многочлена увеличивается на 1. Итерационный процесс продолжается до получения заданной точности.
Для построения многочленов Эрмита нечетной степени 2k-1 используются значения функции и ее производной во всех k узлах, для построения многочленов четной степени 2k используется значение функции в k узлах и значение производной в k-1 узле.
Вычисления производятся по треугольной итерационной схеме Эйткена:
x1 y1 V1 V12 V13 V14 V15 ... V1,2m-1
y1' V2 V23 V24 V25 ...
x2 y2 V3 V34 V35 ...
y2' V4 V45 ...
x3 y3 V5 ...
y3' ...
. . . . . . . . . . . . . . . . . .
xm ym V2m-1
ym'
Элементы V1, V12, ..., V2m-1 первой строки этой схемы представляют собой значения многочленов Эрмита последовательно возрастающих степеней:
V1 = H(1)(x), V12 = H(2)(x), ..., V1,2n-1 = H(2m-1)(x).
Элементы первого столбца V1, V2, ..., V2m-1 вычисляются по формулам:
Vi = yj + yj'(x - xj)
Vi+1 = yj + (yj+1 - yj)[(x - xj)/(xj+1 - xj)],
где i=1, 3, 5, ..., 2m-1, и j=(i+1)/2. Остальные элементы этой схемы вычисляются (вверх по диагонали) по следующей рекуррентной формуле:
![]()
где j=(i+1)/2, l=(k+3)/2.
Для определения значений многчлена H(k)(x) при росте k в вычислительный процесс вовлекаются все более удаленные от x узлы интерполяции. Поэтому значения xk, yk и yk' (k=1, 2, ..., m) предварительно упорядочиваются таким образом, чтобы модули разностей |xk - x| возрастали при росте индекса k:
|xk - x| ≤ |xk+1 - x|.
Вызов программы
CALL PL12(X, Y, DY, XX, M, Eps, YY, Error)
Параметры программы
X, Y, DY, XX, M, Eps - входные параметры;
YY, Error - выходные параметры;
Real X(1:N), Y(1:N), DY(1:N) - массивы, содержащие значения аргумента, функции и производной. Массив X должен быть упорядочен в возрастающем порядке;
Real XX - значение аргумента, в котором требуется вычислить значение функции, X[1] <= XX <= X[N];
Integer M - число узлов, которое разрешается использовать при интерполяции, 1 <= M <= N;
Real Eps - погрешность, с которой требуется вычислить значение функции;
Real YY - значение функции, вычисляемое программой;
Integer Error - индикатор ошибки, принимающий при выполнении программы одно из следующих значений:
Error=0 - заданная точность интерполяции достигнута, ошибок нет;
Error=1 - заданная точность не достигается или достигнутая точность не может быть проверена, т.к. мало значение M;
Error=2 - заданная точность не достигается из-за роста вычислительной погрешности или плохого поведения старших производных интерполируемой функции.
Пример
! Интерполяция функции многочленом Эрмита
! по интерполяционной схеме Эйткена.
program TestPL12
use NML_PL12
implicit none
integer, parameter:: n=40
real:: X(n), Y(n), DY(n), XX, YY, YE, Eps
integer:: M, Er
integer i
!begin
M=6
Eps=1.E-8
do i=1, n
X(i)=0.5*float(i-1)
Y(i)=exp(-X(i))*sin(X(i))
DY(i)=exp(-X(i))*(-sin(X(i))+cos(X(i)))
end do
XX=5.2
YE=exp(-XX)*sin(XX)
call PL12(X, Y, DY, XX, M, Eps, YY, Er)
print 10, Er
print 11, XX, YE, YY
10 format(/' Error =',I2/)
11 format(' X = ',F6.2,' YE =',F11.6,' YY =',F11.6/)
end program TestPL12
────────────
Error = 0
X = 5.20 YE = -0.004874 YY = -0.004874
SPL
Программа SPL вычисляет коэффициенты кубического интерполяционного сплайна для функциональной зависимости yi = y(xi), i=1, 2, ..., n. Кубический сплайн представляет собой многочлен третьей степени на каждом из отрезков [xi, xi+1], i=1, 2, ..., n-1:
│s1(x) = y1 + b1(x - x1) + c1(x - x1)2 + d1(x - x1)3
│ . . . . . . . . . . . . . . . . . . . .(1)
│sn-1(x) = yn-1 + bn-1(x - xn-1) + cn-1(x - xn-1)2 + dn-1(x - xn-1)3
Для нахождения коэффициентов сплайна bi, ci, di используют условия сшивания для самих многочленов и для их первой и второй производной в точке xi:
│s1(x2) = y1 + b1h1 + c1h12 + d1h13 = y2
│ . . . . . . . . . . . . . . . . . . . .(2)
│sn-1(xn) = yn-1 + bn-1hn-1 + cn-1hn-12 + dn-1hn-13 = yn
│s1'(x2) = s2'(x2)
│ . . . . . . . . . . .(3)
│sn-2'(xn-1) = sn-1'(xn-1)
│s1"(x2) = s2"(x2)
│ . . . . . . . . . . .(4)
│sn-2"(xn-1) = sn-1"(xn-1)
где h1 = x2 - x1, ..., hn-1 = xn - xn-1. Из (4) получаем:
│c1 + 3d1h1 = c2
│ . . . . . . .
│cn-2 + 3dn-2hn-2 = cn-1
и дополняем уравнением cn-1 + 3dn-1hn-1 = cn. Вводим обозначения
│c1 = 3σ1
│ . . .
│cn = 3σn
│∆1 = (y2 - y1)/h1
│ . . . . . . .
│∆n-1 = (yn - yn-1)/hn-1
Имеем с помощью (2):
│bi = ∆i - hi(σi+1 + 2σi)
│ci = 3σi i=1, ..., n-1
│di = (σi+1 - σi)/hi
Подставляем в (3) с учетом (2):
│h1σ1 + 2(h1 + h2)σ2 + h2σ3 = ∆2 - ∆1
│h2σ2 + 2(h2 + h3)σ3 + h3σ4 = ∆3 - ∆2
│ . . . . . . . . . . . . . . . . . . . .(5)
│hn-3σn-3 + 2(hn-3 + hn-2)σn-2 + hn-2σn-1 = ∆n-2 - ∆n-3
│hn-2σn-2 + 2(hn-2 + hn-1)σn-1 + hn-1σn = ∆n-1 - ∆n-2
Мы получили систему из n-2 уравнений и n неизвестных.
Дополним полученную систему (5) уравнениями s1"(x1) = 0 и sn-1"(xn) = 0, или, что то же самое, σ1=σn=0. Тогда получаем полную систему для определения неизвестных bi, ci, di коэффициентов сплайна (1). Матрица полученной системы является симметричной и с диагональным преобладанием.
Построенный сплайн минимизирует функционал
b
J(s) = ∫(s"(x))2dx,
a
где a=x1, b=xn.
Применение краевых условий s1"(x1)=0 и sn-1"(xn)=0 не является оптимальным, поскольку в этом случае значение сплайна вблизи граничных точек может сильно отличаться от значения интерполируемой функции. Поэтому в программе применяются следующие типы краевых условий:
- краевые условия 1-го типа. s'(a) = y'(a), s'(b) = y'(b) - на концах промежутка [a,b] задаются значения 1-ой производной интерполируемой функции;
- краевые условия 2-го типа. s"(a) = y"(a), s"(b) = y"(b) - на концах промежутка [a,b] задаются значения 2-ой производной интерполируемой функции;
- краевые условия 3-го типа. s'(a) = s'(b), s"(a) = s"(b) - периодические краевые условия, которые применяются в случае, если интерполируемая функция является периодической с периодом T=b-a;
- краевые условия 4-го типа. Применяются, когда неизвестны ни первые, ни вторые производные в граничных точках и функция не является периодической. В этом случае недостающие два уравнения получаются из аппроксимации третьих производных на концах промежутка по четырем первым и четырем последним из заданных точек.
Недостающие уравнения выглядят следующим образом:
для краевых условий 1 типа
2h1σ1 + h1σ2 = ∆1 - y'(x1),
hn-1σn-1 + 2hn-1σn = y'(xn) - ∆n-1;
для краевых условий 2 типа
6σ1 = y"(x1), 6σn = y"(xn);
для краевых условий 3 типа
2(h1 + hn-1)σ1 + h1σ2 + hn-1σn-1 = ∆1 - ∆n-1,
σ1 = σn;
для краевых условий 4 типа
-h1σ1 + h1σ2 = h12∆1(3),
hn-1σn-1 - hn-1σn = hn-12∆n-3(3),
где ∆1(3) = [(∆3 - ∆2)/(x4 - x2) - (∆2 - ∆1)/(x3 - x1)]/(x4 - x1), ∆n-3(3) = [(∆n-1 - ∆n-2)/(xn - xn-2) - (∆n-2 - ∆n-3)/(xn-2 - xn-3)]/(xn - xn-3) - аппроксимации третьих производных.
Вызов программы
CALL SPL(X, Y, ib, D1, DN, B, C, D)
Параметры программы
X, Y, ib, D1, DN - входные параметры;
B, C, D - выходные параметры.
Real X(1:N), Y(1:N) - массивы, содержащие значения аргумента и функции. Массив X должен быть упорядочен в возрастающем порядке;
Integer Ib - параметр, который задает тип граничных условий, 1<=Ib<=4;
Real D1, DN - значения этих параметров используются в граничных условиях 1 и 2 типа;
Real B(1:N), C(1:N), D(1:N) - массивы, содержащие коэффициенты сплайна;
При работе программы SPL используется программа LA30.
SPF
Функция SPF вычисляет значение интерполяционного (SPL) или сглаживающего (SPS) сплайна в заданной точке X.
Для поиска прмежутка [xi..xi+1], в который попадает точка X, применяется двоичный поиск. Программа запоминает во внутренней переменной L номер промежутка, в котором вычислялся сплайн при предыдущем вызове. Если при последующем вызове точка X попадает в тот же промежуток, то повторно промежуток можно не искать и сплайн вычисляется быстрее.
Вызов функции
SPF(X, Y, B, C, D, XX, Id)
Параметры программы
X, Y, B, C, D, XX, Id - входные параметры;
Real Spf - возвращаемое значение.
Real X(1:N), Y(1:N) - массивы, содержащие значения аргумента и функции;
Real B(1:N), C(1:N), D(1:N) - массивы, содержащие значения коэффициентов сплайна;
Real XX - значение аргумента, в котором требуется вычислить значение функции;
Integer Id - параметр, задающий режим вычисления:
id=0 - программа вычисляет значение функции;
id=1 - программа вычисляет значение первой производной;
id=2 - программа вычисляет значение второй производной.
Пример
!Сплайн - интерполяция
program TestSPL
use NML
implicit none
integer, parameter:: n=60
real:: X(n), Y(n), B(n), C(n), D(n), XX, YY, YD, SY, SD
real, parameter:: pi=3.14159265359
integer:: ib=4
real:: H, D1, DN
integer i
!begin
H=2.0*pi/float(n-1)
do i=1, n
X(i)=H*float(i-1)
Y(i)=exp(-X(i))*sin(X(i))
end do
XX=1.2
YY=exp(-XX)*sin(XX)
YD=exp(-XX)*(cos(XX)-sin(XX))
if (ib==1) then
D1=1.0 ! D1=exp(0)*(cos(0)-sin(0))
DN=exp(-2.*pi) ! DN=exp(-2pi)*(cos(2pi)-sin(2pi))
else if (ib==2) then
D1=-2.0 ! D1=-2*exp(0)*cos(0);
DN=-2.*exp(-2.*pi) ! DN=-2*exp(-2pi)*cos(2pi)
else
D1=0.0; DN=0.0
end if
call SPL(X, Y, ib, D1, DN, B, C, D)
SY=SPF(X, Y, B, C, D, XX, 0)
SD=SPF(X, Y, B, C, D, XX, 1)
print 10, XX, YY, YD
print 11, SY, SD
10 format(/' X = ',F6.2,' YY =',F12.7,' YD =',F12.7)
11 format(/16x,'SY =',F12.7,' SD =',F12.7)
end program TestSPL
X = 1.20 YY = 0.2807248 YD = -0.1715847
SY = 0.2807250 SD = -0.1715749
SPS
Программа SPS вычисляет коэффициенты кубического сглаживающего сплайна для функциональной зависимости yi = y(xi), i=1, 2, ..., n. Предполагается, что точные значения yi неизвестны, а заданы с некоторой погрешностью ρi, 0 ≤ ρi ≤ 1. В случае, если все ρi=0, то коэффициенты ai совпадают с yi и сглаживающий сплайн превращается в интерполяционный. Это означает, что чем точнее заданы величины yi, тем меньше должны быть соответствующие значения ρi. Если же требуется, чтобы сплайн прошел в точности через точку (xi,yi), то соответствующую ей погрешность ρi следует положить равной нулю.
Кубический сплайн представляет собой многочлен третьей степени на каждом из отрезков [xi, xi+1], i=1, 2, ..., n-1:
si(x) = ai + bi(x - xi) + ci(x - xi)2 + di(x - xi)3.
Для нахождения коэффициентов сплайна ai, bi, ci, di используются условия сшивания для самих многочленов и для их первой и второй производной в точках xi:
│s1(x2) = a1 + b1h1 + c1h12 + d1h13 = s2(x2) = a2
│ . . . . . . . . . . . . . . . . . . . .
│sn-1(xn) = an-1 + bn-1hn-1 + cn-1hn-12 + dn-1hn-13 = sn(xn) = an
│s1'(x2) = b1 + 2c1h1 + 3d1h12 = s2'(x2) = b2
│ . . . . . . . . . . . . . . . . . . . .
│sn-2'(xn-1) = bn-2 + 2cn-2hn-2 + 3dn-2hn-22 = sn-1'(xn-1) = bn-1
│s1"(x2) = 2c1 + 6d1h1 = s2"(x2) = 2c2
│ . . . . . . . . . . . . . . . . . . . .
│sn-2"(xn-1) = 2cn-2 + 6dn-2hn-2 = sn-1"(xn-1) = 2cn-1
где h1 = x2 - x1, ..., hn-1 = xn - xn-1. Дополнительно n уравнений получают из условия минимизации функционала
bn
J(s) = ∫(s"(x))2dx + ∑(1/ρi)(si - yi)2, x1=a, xn=b,
ai=1
которые имеют вид [Б5]:
│s1(x1) + ρ1s1'''(x1+) = y1
│s2(x2) + ρ2(s2'''(x2+) - s2'''(x2-)) = y2
│ . . . . . . . . . . . . . . . . . . . .
│sn-1(xn-1) + ρn-1(sn-1'''(xn-1+) - sn-1'''(xn-1-)) = yn-1
│sn(xn) - ρnsn'''(xn-) = yn
где si'''(xi+) и si'''(xi-) означают третью производную в точке xi справа и слева.
Введя обозначения
│c1 = 3σ1
│ . . .
│cn = 3σn
│∆1 = (y2 - y1)/h1
│ . . . . . . .
│∆n-1 = (yn - yn-1)/hn-1
и выполнив элементарные преобразования (см. прогр. SPL), получаем следующую систему уравнений:
│D2σ1 + A2σ2 + B2σ3 + C2σ4 = G2
│E3σ1 + D3σ2 + A3σ3 + B3σ4 + C3σ5 = G3
│ . . . . . . . . . . . .(*)
│En-2σn-4 + Dn-2σn-3 + An-2σn-2 + Bn-2σn-1 + Cn-2σn = Gn-2
│En-1σn-3 + Dn-1σn-2 + An-1σn-1 + Bn-1σn = Gn-2
где
Ai = 2(hi-1 + hi) + pi-1/(hi-1)2 + pi(1/hi-1 + 1/hi)2 + pi+1/(hi)2, i=2, ..., n-1
Bi = hi - (1/hi)[pi(1/hi-1 + 1/hi) + pi+1(1/hi + 1/hi+1)], i=2, ..., n-2
Bn-1 = hn-1 - (1/hn-1)[pn-1(1/hn-2 + 1/hn-1) + pn/hn-1]
Ci = pi+1/(hihi+1), i=2, ..., n-2
D2 = h1 - (1/h1)[p1/h1 + p2(1/h1 + 1/h2)]
Di = hi-1 - (1/hi-1)[pi-1(1/hi-2 + 1/hi-1) + pi(1/hi-1 + 1/hi)], i=3, ..., n-1
Ei = pi-1/(hi-2hi-1), i=3, ..., n-1
Gi = ∆i - ∆i-1, i=2, ..., n-1
Здесь pi = 6ρi.
Мы получили систему n-2 уравнений относительно n неизвестных. Недостающие два уравнения получаются из того или иного типа краевых условий.
Краевые условия 1-го типа. s'(a)=y'(a), s'(b)=y'(b) - на концах промежутка [a,b] задаются значения 1-ой производной сглаживаемой функции.
Краевые условия 2-го типа. s"(a)=y"(a), s"(b)=y"(b) - на концах промежутка [a,b] задаются значения 2-ой производной сглаживаемой функции.
Краевые условия 3-го типа. s(a)=s(b), s'(a)=s'(b), s"(a)=s"(b) - периодические краевые условия, которые применяются в случае, если сглаживаемая функция является периодической с периодом T=b-a.
Если значения ни первых, ни вторых производных на концах промежутка не известны и функция не является периодической, то следует положить s"(a)=s"(b)=0, в этом случае достигается эффект наилучшего сглаживания исходной таблично-заданной зависимости.
Недостающие уравнения выглядят следующим образом.
Для краевых условий 1-го и 2-го типа:
│A1σ1 + B1σ2 + + C1σ3 = G1
│Enσn-2 + Dnσn-1 + Anσn = Gn
Значения коэффициентов для краевых условий первого типа:
A1 = 2h1 + (p1 + p2)/(h1)2
B1 = h1 - p1/(h1)2 - p2(1/h1)(1/h1) + 1/h2)
C1 = p2/(h1h2)
En = pn-1/(hn-2hn-1)
Dn = hn-1 - pn-1(1/hn-1)(1/hn-2) + 1/hn-1) - pn/(hn-1)2
An = 2hn-1 + (pn-1 + pn)/(hn-1)2
G1 = ∆1 - y'(a), Gn = y'(b) - ∆n-1.
Значения коэффициентов для краевых условий второго типа:
A1=An=6, B1=C1=En=Dn=0, G1=y"(a), Gn=y"(b).
Краевые условия 3-го типа образуют сисему n-1 уравнений относительно n-1 неизвестного, поскольку в этом случае σ1=σn.
│A1σ1 + B1σ2 + C1σ3 + E1σn-1 + D1σn = G1
│D2σ1 + A2σ2 + B2σ3 + C2σ4 + E2σn = G2
│E3σ1 + D3σ2 + A3σ3 + B3σ4 + C3σ5 = G3
│ . . . . . . . . . . . . . . . .
│En-3σn-5 + Dn-3σn-4 + An-3σn-3 + Bn-3σn-2 + Cn-3σn-1 = Gn-3
│Cn-2σ1 + En-2σn-4 + Dn-2σn-3 + An-2σn-2 + Bn-2σn-1 + = Gn-2
│Bn-1σ1 + Cn-1σ2 + En-1σn-3 + Dn-1σn-2 + An-1σn-1 = Gn-1,
где
A1 = 2(hn-1 + h1) + pn-1/(hn-1)2 + p1(1/hn-1 + 1/h1)2 + p2/(h1)2,
An-1 = 2(hn-2 + hn-1) + pn-2/(hn-2)2 + pn-1(1/hn-2 + 1/hn-1)2 + p1/(hn-1)2,
B1 = h1 - (1/h1)[p1(1/hn-1 + 1/h1) + p2(1/h1 + 1/h2)],
Bn-1 = hn-1 - (1/hn-1)[pn-1(1/hn-2 + 1/hn-1) + p1(1/hn-1 + 1/h1)],
C1 = p2/(h1h2),
Cn-1 = p1/(hn-1h1),
Ai, Bi, Ci, i=2, ..., n-2 совпадает с (*),
D1 = Bn-1, D2 = B1, E1 = Cn-2, E2 = Cn-1,
Di+1 = Bi, Ei+1 = Ci-1, i=2, ..., n-2.
Коэффициенты сплайна находятся из уравнений:
│ai = yi - ρiHi
│bi = ∆i - hi(σi+1 + 2σi) - (1/hi)(pi+1Hi+1 - piHi)
│ci = 3σi
│di = (σi+1 - σi)/hi, i=1, ..., n-1,
an = yn - ρnHn,
где H1 = (σ2 - σ1)/h1, Hi = (σi+1 - σi)/hi - (σi - σi-1)/hi-1 i=2, ..., n-1, Hn = (σn - σn-1)/hn.
Вызов программы
CALL SPS(X, Y, P, ib, D1, DN, A, B, C, D)
Параметры программы
X, Y, P, ib, D1, DN - входные параметры;
A, B, C, D - выходные параметры.
Real X(1:N), Y(1:N) - массивы, содержащие значения аргумента и функции. Массив X должен быть упорядочен в возрастающем порядке;
Real P(1:N) - массив, содержащий значения весовых коэффициентов, 0<=P(i)<=6. Значение P(i) должно быть равно 0, если значение ординаты Y(i) известно точно и должно равняться 6, если значение Y(i) нужно игнорировать;
Integer Ib - параметр, который задает тип граничных условий, 1<=Ib<=4;
Real D1, DN - значения этих параметров используются в граничных условиях 1 и 2 типа;
Real A(1:N), B(1:N), C(1:N), D(1:N) - массивы, содержащие коэффициенты сплайна;
При работе программы SPS используется программа LA31.
Замечание (Сен.2024) Если ваш компилятор не компилирует строчку call random_seed(put=seed), сделайте в ней вызов функции без аргумента call random_seed().
Пример
! Построение сглаживающего сплайна
! и графика сглаженной функции.
module SplPar
integer, parameter:: n=20
real:: X(n), Y(n), P(n), A(n), B(n), C(n), D(n)
integer:: ib
real:: D1, DN
end module SplPar
program TestSPS
$objcomment lib: "D:/Fortran/Bib_GR/Debug/Graphica"
use SplPar
use NML
implicit none
real, parameter:: pi=3.14159265359
integer:: seed(1)
real:: Q(n)
real:: H, AX=0.0, BX=2.0*pi
real, external:: FS
integer i, j
!begin
ib=2
P(:)=0.4
seed(1)=6
call random_seed(put=seed)
call random_number(Q)
H=(BX-AX)/float(n-1)
do i=1, n
X(i)=H*float(i-1)
Y(i)=sin(X(i))+0.2*(Q(i)-0.5)
end do
if (ib==1) then
D1=1.0
DN=1.0
else if (ib==2) then
D1=0.0
DN=0.0
else
D1=0.0; DN=0.0
end if
call SPS(X, Y, P, ib, D1, DN, A, B, C, D)
call Graphic(X(1), X(n), FS)
!график выведен в файл 'gf.txt'
end program TestSPS
real function FS(XX)
use SplPar
use NML
real, intent(in):: XX
FS=SPF(X, A, B, C, D, XX, 0)
return
end
SPL1R
Программа SPL1R вычисляет коэффициенты кубического интерполяционного сплайна для функциональной зависимости yi = y(xi), i=1, 2, ..., n, заданной на сетке ω a = x1 < x2 < ... < xn-1 < xn = b. Кубический сплайн представляет собой многочлен третьей степени на каждом из отрезков [xi, xi+1], i=1, 2, ..., n-1. В отличии от программы SPL (см. выше), число величин, определяющих сплайн, равно n+1, а не 4n.
На каждом из промежутков [xi, xi+1], i=1, 2, ..., n-1, интерполяционная сплайн-функция ищется в виде [Б5]:
Si(x) = yi(1-t)2(1+2t) + yi+1t2(3-2t) + sihit(1-t)2 - si+1t2(1-t)
Здесь hi = xi+1 - xi, t = (x - xi)/hi, а числа si i=1, 2, ..., n являются решением системы линейных алгебраических уравнений, вид которой зависит от типа граничных (краевых) условий. Конкретный вид системы уранений для всех типов граничных условий и алгоритм её решения приведён в [Б5].
Граничные (краевые) условия 1-го типа
S'(a) = f'(a), S'(b) = f'(b)
- на концах промежутка [a,b] задаются значения 1-ой производной интерполируемой функции.
Граничные (краевые) условия 2-го типа
S"(a) = f"(a), S"(b) = f"(b)
- на концах промежутка [a,b] задаются значения 2-ой производной интерполируемой функции.
Граничные (краевые) условия 3-го типа
S(a) = S(b), S'(a) = S'(b), S"(a) = S"(b)
- называются периодическими. Выполнения этих условий естественно требовать в тех случаях, когда интерполируемая функция является периодической с периодом T = b-a.
Граничные (краевые) условия 4-го типа
S(3)(x1 - 0) = S(3)(x1 + 0), S(3)(xn-1 - 0) = S(3)(xn-1 + 0)
требуют особого комментария.
Комментарий. Во внутренних узлах сетки 3-я производная функции S(x), вообще говоря, разрывна. Однако число разрывов 3-й производной можно уменьшить при помощи условий 4-го типа. В этом случае построенный сплайн будет трижды непрерывно дифференцируем на промежутках [x1, x3] и [xn-2, xn].
Окт.2024
Вызов программы
call SPL1R(n,x,y,ind,ib,ax,bx,z,xx,sp,dsp,d2sp)
Параметры программы
n,x,y,ind,ib,ax,bx,xx - входные параметры;
z - входной и выходной параметр;
sp,dsp,d2sp - выходные параметры.
integer n - число узлов;
real x[1:n] - массив дины n, содержит координаты узлов сетки;
real y[1:n] - массив дины n, содержит значения функции в узлах сетки;
integer ind - режим выполнения; ind=0 - программа вычисляет коэффициенты сплайна, ind=1 - программа вычисляет значение сплайна в заданной точке xx;
integer ib - тип граничных условий на границах x=ax, x=bx; ib = 1..4;
real ax,bx - параметры, задающие граничные значения для условий 1-го и 2-го типа;
real xx - координата точки, в которой будет вычислено значение сплайна;
real z[1:n] - массив дины n, после первого вызова с ind=0 содержит коэффициенты сплайна;
real sp - значение сплайна в точке xx;
real dsp - значение 1-й производной сплайна в точке xx;
real d2sp - значение 2-й производной сплайна в точке xx;
При работе программы SPL1R используется программа LA30.
Пример
program Test_SPL1
use NML, only: LA30, SPL1R
implicit none
integer, parameter:: n=21
real:: x(n), y(n), z(n)
integer:: ind, ib
real:: ax, bx, xx, sp, dsp, d2sp
real, parameter:: pi=3.14159265359
real:: h, hd2, del0, del1, del2, yy, d1, d2
integer:: j, nm1
!begin
ind=0 ! вычисляем коэффициенты сплайна
! На отрезке [0, 2π] стрлим равномерную сетку из n узлов
! и вычисляем значения функции y=sin(x) в этих узлах
nm1 = n-1
h=2.0*pi/nm1
do j=1, n
x(j)=h*(j-1)
y(j)=sin(x(j))
enddo
ib=1 ! граничные условия
ax=1.0; bx=1.0 ! граничные значения
call SPL1R(n,x,y,ind,ib,ax,bx,z,xx,sp,dsp,d2sp)
! В массиве z коэффициенты сплайна
ind=1 ! вычисляем значение сплайна в точке xx
! sp, dsp, d2sp - значения функции, 1-ой и 2-ой производной
hd2=0.5*h
del0=0.0; del1=0.0; del2=0.0
! Строим сетку со смещением на h/2 от исходной
! Вычисляем сплайн и производные в новой сетке
do j=1, nm1
xx=h*(j-1)+hd2
yy=sin(xx); d1=cos(xx); d2=-yy
call SPL1R(n,x,y,ind,ib,ax,bx,z,xx,sp,dsp,d2sp)
if(abs(yy-sp) > del0) del0=abs(yy-sp)
if(abs(d1-dsp) > del1) del1=abs(d1-dsp)
if(abs(d2-d2sp) > del2) del2=abs(d2-d2sp)
enddo
! Печать результатов
print *,' n = ', n
print *,' Boundary conditions, ib =', ib
print *,' max|f(x) - S(x)| = ', del0
print *,' max|f''(x) - S''(x)| = ', del1
print *,' max|f"(x) - S"(x)| = ', del2
end program Test_SPL1
n = 21
Boundary conditions, ib = 1
max|f(x) - S(x)| = 2.56896019E-05
max|f'(x) - S'(x)| = 2.23517418E-05
max|f"(x) - S"(x)| = 4.11111116E-03
SPL2R
Программа SPL2R вычисляет коэффициенты бикубического интерполяционного сплайна для функциональной зависимости zi = f(xi, yj), i=1, 2, ..., m, j=1, 2, ..., n, заданной на прямоугольной сетке ω a = x1 < x2 < ... < xm-1 < xm = b, c = y1 < y2 < ... < yn-1 < yn = d. Алгоритм нахождения коэффициентов интерполяционных сплайн-функций приведён в [Б5].
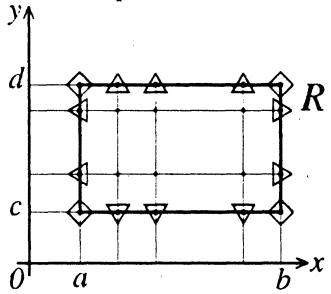
При построении интерполяционного бикубического сплайна наиболее часто используются граничные условия следующих 4-х типов.
Граничные (краевые) условия 1-го типа
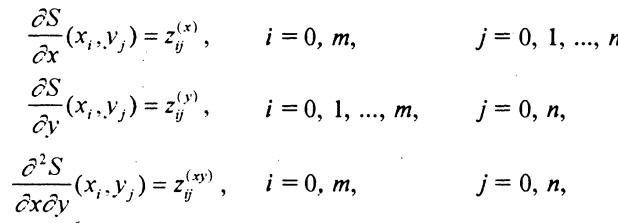
- в граничных узлах сетки ω задаются значения первых частных производных по x и по y интерполируемой функции, а в угловых точках - значения 2-ой смешаной производной. На рисунке жирными точками отмечены внутренние узлы сетки, в которых задаются значения функции S, горизонтальными и вертикальными треугольниками-стелками указаны узлы, в которых задаются значения первых частных производных Sx и Sy соответственно, а ромбиком - значения смешанной производной Sxy.
Граничные (краевые) условия 2-го типа
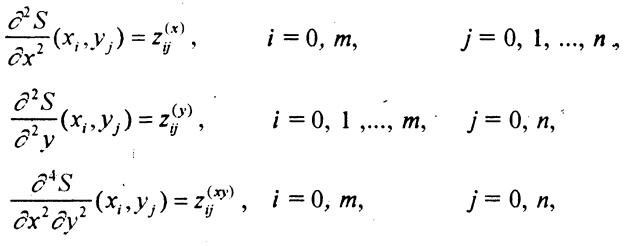
- в граничных узлах сетки ω задаются значения вторых частных производных по x и по y интерполируемой функции, а в угловых точках - значения смешаной производной Sxxyy. На рисунке жирными точками отмечены внутренние узлы сетки, в которых задаются значения функции S, горизонтальными и вертикальными треугольниками-стелками указаны узлы, в которых задаются значения вторых частных производных Sxx и Syy соответственно, а ромбиком - значения смешанной производной Sxxyy.
Граничные (краевые) условия 3-го типа
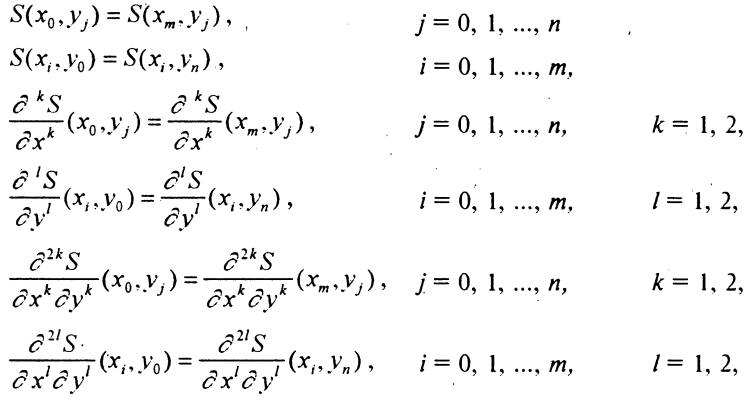
называются периодическими. В этом случае сплайн S(x,y) и его частные производные должны быть двоякопериодическими функциями - с периодом Tx=b-a по переменной x и с пеиодом Ty=d-c по переменной y.
Граничные (краевые) условия 4-го типа
требуют, чтобы на линиях x=x1 и x=xm-1 были непрерывны следующие производные искомого сплайна:
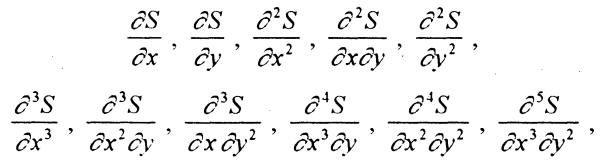
а на линиях y=y1 и y=yn-1 - производные
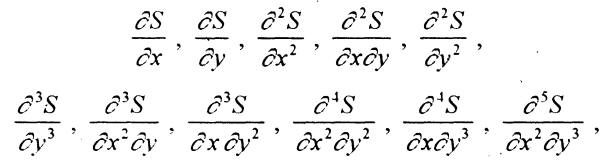
Замечание Кроме перечисленных, возможны и смешанные граничные условия, относящиеся по разным переменным к разным типам. При этом если, например, по переменной x заданы условия 1-го типа, а по переменной y - 2-го типа, то в вершинах прямоугольника R следует задавать частные проихводные Sxyy и т.д.
Окт.2024
Вызов программы
call SPL2R(m,x,n,y,z,ind,ibx,iby,sl,sr,sd,su,sxy,zx,zy,zxy,xx,yy,spl)
Параметры программы
m,n,x,y,z,ind,ibx,iby,sl,sr,sd,su,xx,yy - входные параметры;
zx,zy,zxy - входные и выходные параметры;
spl - выходной параметр.
integer m - число узлов сетки по оси x;
real x[1:m] - массив дины m, содержит координаты узлов сетки по оси x;
integer n - число узлов сетки по оси y;
real y[1:n] - массив дины n, содержит координаты узлов сетки по оси y;
real z[1:m*n] - массив дины m*n, содержит значения интерполируемой функции в узлах сетки; значение функции в узле (i,j) находится в элементе z[i+(j-1)*m];
integer ind - режим выполнения; ind=0 - программа вычисляет коэффициенты сплайна, ind=1 - программа вычисляет значение сплайна в заданной точке (xx,yy);
integer ibx - тип граничных условий на границах x=x1, x=xm; ibx = 1..4;
real sl[1:n] - массив дины n, элемент sl[j] содержит значение j-ой частной производной по x в узлах (1,j) для граничных условий 1-го или 2-го типа;
real sr[1:n] - массив дины n, элемент sr[j] содержит значение j-ой частной производной по x в узлах (m,j) для граничных условий 1-го или 2-го типа;
integer iby - тип граничных условий на границах y=y1, y=yn; iby = 1..4;
real sd[1:m] - массив дины m, элемент sd[i] содержит значение i-ой частной производной по y в узлах (i,1) для граничных условий 1-го или 2-го типа;
real su[1:m] - массив дины m, элемент su[i] содержит значение i-ой частной производной по y в узлах (i,n) для граничных условий 1-го или 2-го типа;
real sxy[1:4] - массив дины 4, содержит значения смешанных производных в угловых точках для граничных условий 1-го или 2-го типа;
real zx[1:m*n], zy[1:m*n], zxy[1:m*n] - массивы дины m*n, содержит значения параметров сплайна;
real xx,yy - координаты точки, в которой будет вычислено значение сплайна;
real spl - вычисленное значение сплайна в точке (xx,yy);
При работе программы SPL2R используются программы LA30 и SPL1R.
Пример
program Test_SPL2R
use NML, only: LA30, SPL1R, SPL2R
implicit none
integer, parameter:: m=21, n=11, mn=m*n
real:: x(m), y(n), z(mn)
integer:: ind, ibx, iby
real:: sl(n), sr(n), sd(m), su(m), sxy(4)
real:: zx(mn), zy(mn), zxy(mn), xx, yy, spl
real, parameter:: pi=3.14159265359
integer, parameter:: ks=8
real:: hx, hy, xs(ks), ys(ks), sc(ks), ss(ks), del(ks), hx2, hy2
integer:: i, j, ihx, ihy, k
!begin
ind=0 ! вычисляем параметры сплайна
! Вычисляем функцию f(x,y) = sin(x)*sin(y)
! в прямоугольнике 0≤x≤π, 0≤y≤π/2
ihx=40; ihy=40 ! задают шаг сетки
hx=2.0*pi/ihx; hy=2.0*pi/ihy
do i=1, m
x(i)=hx*(i-1)
enddo
do j=1, n
y(j)=hy*(j-1)
enddo
do j=1, n
do i=1, m
z(i+(j-1)*m)=sin(x(i))*sin(y(j))
enddo
enddo
ibx=1; iby=1 ! граничные условия
do i=1, m
sd(i)=sin(x(i)); su(i)=0.0
enddo
do j=1, n
sl(j)=sin(y(j)); sr(j)=-sin(y(j))
enddo
sxy(1)=1.0; sxy(2)=-1.0; sxy(3)=0.0; sxy(4)=0.0;
call SPL2R(m,x,n,y,z,ind,ibx,iby,sl,sr,sd,su,sxy,zx,zy,zxy,xx,yy,spl)
ind=1 ! вычисляем значение сплайна в точке xx
! xs и ys - координаты точек между узлами сетки
hx2=0.5*hx; hy2=0.5*hy
do k=1, ks
xs(k)=pi/2+hx2+hx*k; ys(k)=hy2+hy*k
sc(k)=sin(xs(k))*sin(ys(k))
call SPL2R(m,x,n,y,z,ind,ibx,iby,sl,sr,sd,su,sxy,zx,zy,zxy,xs(k),ys(k),ss(k))
del(k)=ss(k)-sc(k)
enddo
! Печать результатов
print 10, m, n
print 11, ibx, iby
print 12
print 13, (xs(k),ys(k),sc(k),ss(k),del(k), k=1,ks)
10 format(/4x,'m =',I4,' n =',I4)
11 format(4x,'Boundary conditions, ibx =',I3,' iby =',I3)
12 format(6x,'X',9x,'Y',9x,'Exact',11x,'Spline',10x,'Delta')
13 format(2F10.5,3E16.7)
end program Test_SPL2R
m = 21 n = 11
Boundary conditions, ibx = 1 iby = 1
X Y Exact Spline Delta
1.80642 0.23562 0.2269953E+00 0.2269945E+00 -0.7450581E-06
1.96350 0.39270 0.3535534E+00 0.3535523E+00 -0.1162291E-05
2.12058 0.54978 0.4455032E+00 0.4455017E+00 -0.1460314E-05
2.27765 0.70686 0.4938442E+00 0.4938426E+00 -0.1639128E-05
2.43473 0.86394 0.4938442E+00 0.4938425E+00 -0.1609325E-05
2.59181 1.02102 0.4455032E+00 0.4455018E+00 -0.1430511E-05
2.74889 1.17810 0.3535532E+00 0.3535521E+00 -0.1102686E-05
2.90597 1.33518 0.2269950E+00 0.2269943E+00 -0.7599592E-06
SPS1R
Программа SPS1R вычисляет коэффициенты кубического сглаживающего сплайна для функциональной зависимости yi = y(xi), i=1, 2, ..., n, заданной на сетке ω a = x1 < x2 < ... < xn-1 < xn = b. Кубический сплайн представляет собой многочлен третьей степени на каждом из отрезков [xi, xi+1], i=1, 2, ..., n-1.
На каждом из промежутков [xi, xi+1], i=1, 2, ..., n-1, интерполяционная сплайн-функция ищется в виде [Б5]:
Si(x) = zi(1-t) + zi+1t - (hi2/6)t(1-t)((2-t)si + (1+t)si+1)
Здесь hi = xi+1 - xi, t = (x - xi)/hi, а числа zi и si i=1, 2, ..., n являются решением системы линейных алгебраических уравнений, вид которой зависит от типа граничных (краевых) условий. Конкретный вид системы уранений для всех типов граничных условий и алгоритм её решения приведён в [Б5].
Граничные (краевые) условия 1-го типа
S'(a) = f'(a) = y1, S'(b) = f'(b) = yn
- на концах промежутка [a,b] задаются значения 1-ой производной интерполируемой функции.
Граничные (краевые) условия 2-го типа
S"(a) = 0, S"(b) = 0
- на концах промежутка [a,b] 2-е производные интерполируемой функции равны нулю.
Граничные (краевые) условия 3-го типа
S(a) = S(b), S'(a) = S'(b), S"(a) = S"(b)
- называются периодическими. Выполнения этих условий естественно требовать в тех случаях, когда интерполируемая функция является периодической с периодом T = b-a.
Выбор весовых коэффициентов
Выбор весовых коэффициентов ρi позволяет управлять сглаживающим свойством сплайна. Если все ρi=0, то zi=yi и сглаживающий сплайн становится интерполяционым. Чем больше весовой множитель некоторой конкретной точки отличается от нуля, тем менее значение функции в этой точке учитывается при вычислении коэффициентов сплайна.
Окт.2024
Вызов программы
call SPS1R(n,x,y,ind,ib,ax,bx,rho,zs,zm,xx,sp,dsp,d2sp)
Параметры программы
n,x,y,ind,ib,ax,bx,xx,rho - входные параметры;
zs,zm - входные и выходные параметры;
sp,dsp,d2sp - выходные параметры.
integer n - число узлов;
real x[1:n] - массив дины n, содержит координаты узлов сетки;
real y[1:n] - массив дины n, содержит значения функции в узлах сетки;
integer ind - режим выполнения; ind=0 - программа вычисляет коэффициенты сплайна, ind=1 - программа вычисляет значение сплайна в заданной точке xx;
integer ib - тип граничных условий на границах x=ax, x=bx; ib = 1..3;
real ax,bx - параметры, задающие граничные значения для условий 1-го и 2-го типа;
real rho[1:n] - массив дины n, содержит весовые коэффициенты значений функции;
real xx - координата точки, в которой будет вычислено значение сплайна;
real zs[1:n], zm[1:n] - массивы дины n, после первого вызова с ind=0 содержат коэффициенты сплайна;
real sp - значение сплайна в точке xx;
real dsp - значение 1-й производной сплайна в точке xx;
real d2sp - значение 2-й производной сплайна в точке xx;
При работе программы SPS1R используются программы LA31 и SPL1R.
Пример
program Test_SPS1 use NML, only: LA31, SPS1R implicit none integer, parameter:: n=21 real:: x(n), y(n), z(n), rho(n), zs(n), zm(n), R(n) integer:: ind, ib real:: ax, bx, xx, sp, dsp, d2sp real, parameter:: pi=3.14159265359 real:: h, hd2, del0, del1, del2, yy, d1, d2, Am integer:: j, nm1 !begin ! Заполнение массива ρ случайными числами из диапазона [0:1) call random_seed() call random_number(R) ! pseudo-random number generator (PRNG) ind=0 ! вычисляем параметры сплайна ! Весовые коэффициенты rho(:)=0.1 ! Амплитуда отклонения значения функции Am=0.1 ! На отрезке [0, 2π] стрлим равномерную сетку из n узлов ! и вычисляем значения функции y=sin(x) в этих узлах nm1 = n-1 h=2.0*pi/nm1 do j=1, n x(j)=h*(j-1) y(j)=sin(x(j))+Am*(R(j)-0.5) enddo ib=1 ! граничные условия ax=1.0; bx=1.0 ! граничные значения call SPS1R(n,x,y,ind,ib,ax,bx,rho,zs,zm,xx,sp,dsp,d2sp) !SPS1R(n,x,y,rho,zs,zm,ind,ib,ax,bx,xx,sp,dsp,d2sp) ! В массиве zs параметры сплайна ind=1 ! вычисляем значение сплайна в точке xx ! sp, dsp, d2sp - значения функции, 1-ой и 2-ой производной hd2=0.5*h del0=0.0; del1=0.0; del2=0.0 ! Строим сетку со смещением на h/2 от исходной ! Вычисляем сплайн и производные в новой сетке do j=1, nm1 xx=h*(j-1)+hd2 yy=sin(xx); d1=cos(xx); d2=-yy call SPS1R(n,x,y,ind,ib,ax,bx,rho,zs,zm,xx,sp,dsp,d2sp) !SPS1R(n,x,y,rho,zs,zm,ind,ib,ax,bx,xx,sp,dsp,d2sp) if(abs(yy-sp) > del0) del0=abs(yy-sp) if(abs(d1-dsp) > del1) del1=abs(d1-dsp) if(abs(d2-d2sp) > del2) del2=abs(d2-d2sp) enddo ! Печать результатов print *,' n = ', n print *,' Amplitude = ', Am print *,' Weighting factors = ', rho(1) print *,' Boundary conditions, ib =', ib print *,' max|f(x) - S(x)| = ', del0 print *,' max|f''(x) - S''(x)| = ', del1 print *,' max|f"(x) - S"(x)| = ', del2 end program Test_SPS1 n = 21 Amplitude = 0.00000000 Weighting factors = 0.00000000 Boundary conditions, ib = 1 max|f(x) - S(x)| = 2.57492065E-05 max|f'(x) - S'(x)| = 2.24113464E-05 max|f"(x) - S"(x)| = 4.11099195E-03 n = 21 Amplitude = 0.100000001 Weighting factors = 0.100000001 Boundary conditions, ib = 1 max|f(x) - S(x)| = 4.64271307E-02 max|f'(x) - S'(x)| = 6.58317208E-02 max|f"(x) - S"(x)| = 0.141094089 n = 21 Amplitude = 0.200000003 Weighting factors = 0.200000003 Boundary conditions, ib = 1 max|f(x) - S(x)| = 9.76079702E-02 max|f'(x) - S'(x)| = 0.104151309 max|f"(x) - S"(x)| = 0.238730460
Hermite
Задано некоторое множество точек (вершин) P1 ... Pn на плоскости или в пространстве, n>1. Программа Hermite строит составную аппроксимирующую кривую Эрмита γ(1)ᑌ ... ᑌγ(n), которая является объединением элементарных кубических кривых γ(i), i = 1, ..., n-1. Элементарная кубическая кривая Эрмита определяется двумя вершинами Pi и Pi+1 и ненулевыми касательными векторами в этих точках Qi и Qi+1 (Рис 1).
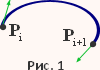
Координаты точек кривой между вершинами Pi и Pi+1 можно найти из векторного уравнения
R(t) = (1 - 3t2 + 2t3) Pi + t2(3 - 2t) Pi+1 + t(1 - 2t + t2) Qi - t2(1 - t) Qi+1, 0 ≤ t ≤ 1
Это уравнение в координатной (матричной) форме может быть записано как
R(t) = GMT, 0 ≤ t ≤ 1
где (для точек P1 и P2)
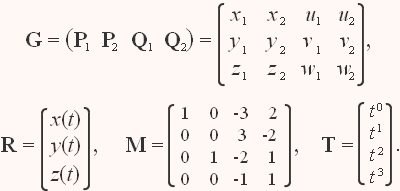
Матрица M называется базисной матрицей кубической кривой Эрмита, а матрица G - её геометрической матрицей. Здесь x, y и z - пространственные координаты вершин P1 и P2, u, v, w - координаты касательных векторов Q1 и Q2.
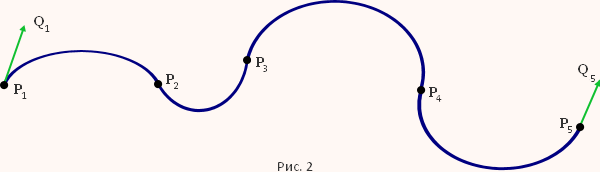
Составная кривая Эрмита (Рис. 2) является объединением элементарных кривых Эрмита и определяется массивом вершин P1 ... Pn, n>1. Каждая i-ая кривая описывается уравнением
R(i)(t) = (Pi Pi+1 Qi Qi+1)MT, 0 ≤ t ≤ 1
где M - базисная матрица, а промежуточные векторы Q2 ... Qn-1 можно найти из условий равенства вторых производных в базисных точках P2 ... Pn-1, которые сводятся к матричному уравнению
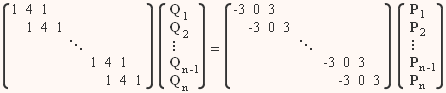
Свойства составной кривой Эрмита описаны в [Б5].
Программная реализация
Для начала вычислений нужно задать вершины, через которые должна пройти кривая, и векторы касательных в конечных вершинах. Программа HermiteTangents вычисляет значения касательных в промежуточных вершинах. Программа Hermite вычисляет координаты заданной точки на построенной кривой. Точка на кривой задаётся параметром t, который должен лежать в пределах от 0 до n-1. Целая часть параметра определяет номер i элементарной кривой Эрмита, а дробная часть задаёт положение точки на этой кривой.
[Б5]
Вызов программы HermiteTangents
call HermiteTangents(XP, xq1, xqN, XQ)
Параметры программы
XP(1:n), xq1, xqN - входные параметры;
XQ(1:n) - выходной параметр.
Real XP(1:n) - массив, содержащий x-, y- или z-координаты точек Pi, i=1, ..., n;
Real xq1, xqN - x-, y- или z-координаты касательных векторов в точках P1 и Pn:
Real XQ(1:n) - массив, содержащий x-, y- или z-координаты касательных векторов Qi в точках Pi, i=1, ..., n;
integer n - задаёт количество точек P и размерность массивов XP и XQ;
Вызов программы Hermite
Hermite(XP, XQ, t)
Программа Hermite должна быть вызвана после вызова программы HermiteTangents
Параметры программы
XP(1:n), XQ(1:n), t - входные параметры;
Real Hermite - возвращаемое значение;
Real XP(1:n) - массив, содержащий x-, y- или z-координаты точек Pi, i=1, ..., n;
Real XQ(1:n) - массив, содержащий x-, y- или z-координаты касательных векторов Qi в точках Pi, i=1, ..., n (вычислены с помощью программы HermiteTangents);
integer n - задаёт количество точек P и размерность массивов XP и XQ;
Real t - значение параметра, в котором нужно найти x-, y- или z-координату составной кривой Эрмита, 0 ≤ t ≤ n-1
Примеры
program TestHermit
! Построение аппроксимирующей кривой Эрмита
use GRAPHICA
use NML
implicit none
integer, parameter:: n=8, div=32
real XP(n), YP(n), XQ(n), YQ(n), xq1, yq1, xqN, yqN
real T(div), XT(div), YT(div), dt
integer i
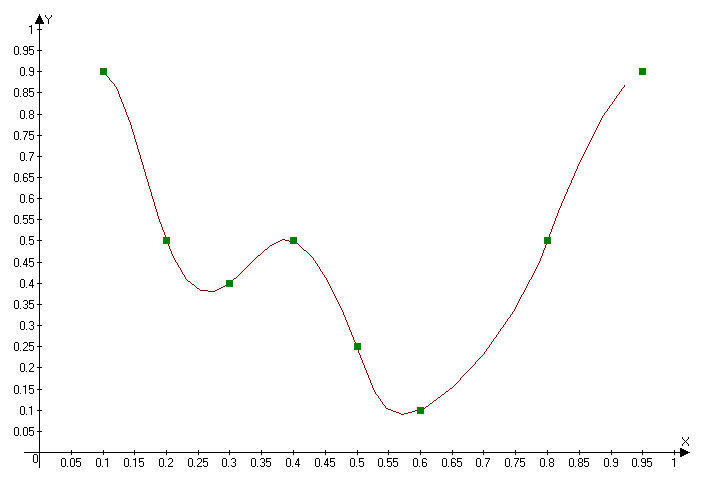
data XP/0.10, 0.20, 0.30, 0.40, 0.50, 0.60, 0.80, 0.95/
data YP/0.90, 0.50, 0.40, 0.50, 0.25, 0.10, 0.50, 0.90/
data xq1/0.1/, yq1/-0.02/, xqN/0.1/, yqN/0.01/
! Вычисление X и Y координат касательных во внутренних точках
call HermiteTangents(XP, xq1, xqN, XQ)
call HermiteTangents(YP, yq1, yqN, YQ)
! Заполнение массива с параметром
dt=float(n-1)/float(div)
do i=1,div
T(i)=(i-1)*dt
enddo
! Построение аппроксимирующей кривой
do i=1,div
XT(i)=Hermite(XP, XQ, T(i))
YT(i)=Hermite(YP, YQ, T(i))
enddo
! Вывод результатов вычислений
print 10
print 11, (T(i), XT(i), YT(i), i=1, div)
call Graphar(XT, YT)
10 format(8X,'t',10X,'x',14X,'y')
11 format(2X,F10.7,2E15.7)
end program TestHermit
График построен программой Advanced Grapher
program TestHermit2
! Построение кривой Эрмита c самопересечением
use GRAPHICA
use NML
implicit none
integer, parameter:: n=8, div=64
real XP(n), YP(n), XQ(n), YQ(n), xq1, yq1, xqN, yqN
real T(div), XT(div), YT(div), dt
integer i
data XP/0.10, 0.30, 0.50, 0.70, 0.95, 0.70, 0.40, 0.10/
data YP/0.30, 0.50, 0.65, 0.55, 0.45, 0.30, 0.30, 0.45/
data xq1/0.05/, yq1/0.02/, xqN/-0.05/, yqN/-0.04/
call HermiteTangents(XP, xq1, xqN, XQ)
call HermiteTangents(YP, yq1, yqN, YQ)
dt=float(n-1)/float(div)
do i=1,div
T(i)=(i-1)*dt
XT(i)=Hermite(XP, XQ, T(i))
YT(i)=Hermite(YP, YQ, T(i))
enddo
! Вывод результатов вычислений
print 10
print 11, (T(i), XT(i), YT(i), i=1, div)
call Graphar(XT, YT)
10 format(8X,'t',10X,'x',14X,'y')
11 format(2X,F10.7,2E15.7)
end program TestHermit2
ORT
Программа ORT осуществляет разложение таблично-заданной зависимости yi=y(xi), i=1, ..., n в ряд по системе многочленов, ортогональных на множестве точек {xi}:
m
y(x) = ∑ αkuk(x),
k=0
где αk - коэффициенты этого разложения, а uk(x) - ортогональные многочлены последовательно возрастающих степеней:
k
uk(x) = ∑ βj(k)xj k=0, ..., m. j=0
Предполагается, что значения yi заданы с некоторой неопределённостью (с весовыми коэффициентами) pi, 0 < pi ≤ 1. Значение pi=1 означает, что соответствующее значение yi задано точно, и наоборот, чем ближе pi к нулю, тем менее учитывается данная точка при аппроксимации. Весовые коэффициенты легко вычислить, если известна погрешность ∆i величин yi, т.е. yi ± ∆i. Тогда весовые коэффициенты будут равны
pi = 1 - (∆i/∆max),
где ∆max - максимальное значение погрешности.
Система ортогональных многочленов строится по рекуррентному соотношению
A*uk+1(x) = (x-A)uk(x) - Buk-1(x), u0=0, u1=1/SQRT(∑pi),
где A=∑pixiuk2(xi), B=∑pixiuk(xi)uk-1(xi). A* находится из условия нормировки
n
∑ piuk+12(xi) = 1.
i=1
Коэффициент разложения αk определяется из формулы
n
αk = ∑ piyiuk(xi).
i=1
Программа последовательно увеличивает количество ортогональных многочленов, участвующих в аппроксимации заданной дискретной зависимости y(xi), пока степень старшего многочлена не достигнет заданного значения m (m≥0) или пока из-за накопления вычислительной погрешности среднеквадратичное отклонение
![]()
не перестанет уменьшаться. Достигнутая программой степень старшего многочлена возвращается в переменной Order.
Для упрощения дальнейших расчетов коэффициенты всех многочленов при одинаковых степенях x суммируются и результатом выполнения программы является массив коэффициентов c0, c1, ..., COrder. Значение функции в точке x (x1 ≤ x ≤ xn) можно вычислить по формуле
Order
y(x) = ∑ ckxk.
k=0
Краткое описание алгоритма построения многочленов, ортогональных на множестве точек, можно найти в [А4], а также в [Б15]. Данный метод более устойчив к накоплению ошибок вычислений, чем метод наименьших квадратов.
Вызов программы
CALL ORT(X, Y, P, C, M, Order, Sigma)
Параметры программы
X, Y, P, M - входные параметры;
C, Order, Sigma - выходные параметры.
Real X(1:N), Y(1:N) - массивы, содержащие значения аргумента и функции. Массив X должен быть упорядочен в возрастающем порядке;
Real P(1:N) - массив, содержащий значения весовых коэффициентов, 1>=P(i)>0. Значение P(i) должно быть равно 1, если значение ординаты Y(i) известно точно и стремиться к 0, если значение Y(i) можно игнорировать;
Real C(0:M) - массив, содержащий коэффициенты многочлена, аппроксимирующего исходную зависимость;
Integer M - наибольшая степень многочлена, которую разрешается достигнуть программе;
Integer Order - наибольшая степень многочлена, которую удалось достигнуть программе, Order ≤ M;
Real Sigma - среднеквадратичное отклонение, достигнутое при аппроксимации.
Пример
! Аппроксимация функции многочленами,
! ортогональными на множестве точек.
module OrtPar
integer, parameter:: M=20
real:: C(0:M)
integer:: Order
end module OrtPar
program TestORT
$objcomment lib: "D:/Fortran/Bib_GR/Debug/Graphica"
use OrtPar
use NML
implicit none
integer, parameter:: n=40
real:: X(n), Y(n), P(n)
data P/n*1.0/
real, external:: OrtPol
real, parameter:: pi=3.1415926
real:: H, XX, YY, YYY, Sigma
integer:: i
!begin
H=2.0*pi/float(n-1)
do i=1, n
X(i)=H*float(i-1)
Y(i)=sin(X(i))
end do
XX=0.5
YY=sin(XX)
call ORT(X, Y, P, C, M, Order, Sigma)
YYY=OrtPol(XX)
print 10, XX, YY, YYY, Order, Sigma
10 format(/' X = ',F6.2,' YY =',F12.7,' YYY =',F12.7 &
/' Order =',I3,' Sigma =',E15.7/)
call Graphic(X(1), X(n), OrtPol)
print 20, (i, C(i), i=0, Order)
20 format(8x,I2,4x,E14.6)
end program TestORT
real function OrtPol(X)
use OrtPar
real, intent(in):: X
real:: S
integer i
S=0.0
do i=Order, 1, -1
S=(S+C(i))*X
end do
OrtPol=S+C(0)
return
end function OrtPol
X = 0.50 YY = 0.4794255 YYY = 0.4794317
Order = 9 Sigma = 0.2819624E-04
0 0.361258E-05
1 0.999756E+00
2 0.152848E-02
3 -0.170313E+00
4 0.445399E-02
5 0.517216E-02
6 0.138082E-02
7 -0.574159E-03
8 0.610403E-04
9 -0.215886E-05
