Zeroin
Программа Zeroin вычисляет корень функции f(x) в заданном интервале [a,b]. Интервал должен содержать не более одного корня функции первой кратности, т.е. f(a) и f(b) должны быть разных знаков.
Для вычисления корня программа использует методы деления отрезка пополам (бисекция), при возмоожности переходит к линейной (метод секущих) или обратной квадратичной интерполяции.
Подробное описание программы "ZEROIN" можно найти в книге [Б3].
Вызов программы
Zeroin(Fun, AX, BX, Eps)
Параметры программы
Fun, AX, BX, Eps - входные параметры;
Real Zeroin - возвращаемое значение;
Real Fun(Real X) - исследуемая функция;
Real AX, BX - границы интервала;
Real Eps - погрешность вычисления корня.
Пример
!Поиск корня нелинейного уравнения
program TestZeroin
use NML
implicit none
integer:: Count=0
real:: A, B, R, Eps
data A/-5.0/, B/5.0/, Eps/1.0E-8/
!begin
R=Zeroin(Fun, A, B, Eps)
print 10, R, Count
10 format(/'Root =',E16.7,' Count =',I3)
contains
real function Fun(x)
real, intent(in):: x
Fun=((x+1.0)*x+2.0)*((x+2.0)*x+2.0)* &
((x-1.0)*x+2.0)*(x-4.0)*((x-8.0)*x+20.0)
Count=Count+1
return
end function Fun
end program TestZeroin
Root = 0.4000000E+01 Count = 13
ZR10
Программа ZR10 вычисляет n корней произвольной функции f(x) при помощи изучения поведения знака функции в интервале [a,b] и дальнейшее их уточнение с точностью до Eps.
Программа "шагает" от точки a к точке b с шагом h. Если функция меняет знак, программа уточняет значение корня с точностью до Eps делением отрезка пополам (бисекция). Используется относительная погрешность (|x - xroot| / |x|) < Eps, в окрестности нуля - абсолютная погрешность |x - xroot| < Eps, а также контролируется значение функции |Fun(x)| < Eps. Не стоит брать значение Eps слишком маленьким. Полученные значения корней следует рассматривать только как приближения к точным значениям и использовать это приближение в других, более быстродействующих, программах (например Zeroin).
b может быть как больше a, так и меньше, в последнем случае программа "шагает" от больших значений аргумента к меньшим. Рекомендуется делать шаг h не больше предполагаемого минимального расстояния между корнями.
Вызов программы
call ZR10(Fun, A, B, H, Eps, C, Cnt)
Параметры программы
Fun, A, B, H, Eps - входные параметры;
Real Fun(Real X) - исследуемая функция;
Real A, B - границы интервала;
Real H - шаг поиска корней;
Real Eps - погрешность вычисления корня;
Real C(N) - массив, в который помещаются найденные корни;
Integer N - количество предполагаемых корней;
Integer Cnt - количество найденных корней.
ZR30
Программа ZR30 вычисляет вещественные корни функции f(x) методом парабол (Мюллера).
На каждой k-ой итерации по трём точкам pk, pk+1, pk+2 строится
интерполяционный полином Лагранжа L(p):
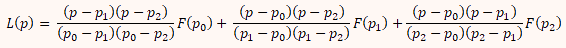
и за следуещее приближение принимается ближайший к pk+2 корень уравнения L(p)=0. Итерационный процесс продолжается, пока приближение к корню не достигнет заданной точности. Если задано начальное приближение к i-му корню ci, то за первые три точки принимаются значения p0=0.9×ci, p1=1.1×ci, p2=1.0×ci. Если ci=0, то в качестве перых трёх точек принимается -1, 1 и 0.
Для облегчения вычислений в программе вводятся следующие переменные:
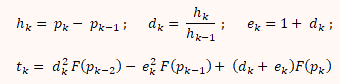
За новую независимую переменную принимается dk. Тогда корни уравнения L(dk)=0 будут равны
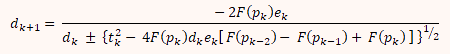
Знак перед фигурной скобкой выбирается так, чтобы модуль знаменателя был наибольшим. Следующая точка в последовательности будет равна
pk+1 = pk + dk+1hk
На каждом шаге вычисляется соотношение | F(pk+1) / F(pk) |. Если это соотношение уменьшается больше чем в 10 раз, то dk+1 делится пополам, а pk+1 пересчитывается с заменой dk+1 на dk+1/2 и так до тех пор, пока соотношение не стане меньше 10.
Функция f(x) может быть произвольного вида (не обязательно полином!)
[Б8]. Алгоритм 25б
Вызов программы
call ZR30(Fun, C, Eps1, Eps2, Eps3, Eta, Max, Cnt)
Параметры программы
Fun, Eps1, Eps2, Eps3, Eta, Max - входные параметры;
Real C[N] - входной и выходной параметр;
Real Fun(Real X) - исследуемая функция;
Real Eps1 - относительный критерий сходимости по величине промежутка, счёт прекращается, если |(pk-1 - pk-1) / pk| < Eps1;
Real Eps2 - абсолютный критерий сходимости по значениям функции;
Real Eps3, Eta - используется для кратных корней таким образом, что если |x - ci| < Eps3, то x заменяется на x+Eta;
Integer Max - максимально допустимое количество итераций;
Real С[N] - на входе: начальные приближения для корней,
на выходе: значения найденных корней;
Integer Сnt[N] - количество итераций при вычислении корня ci.
Пример
program TestZR30
use NML
implicit none
! Variables
integer, parameter:: n=6
real C(n), Eps1, Eps2, Eps3, Eta
integer Cnt(n), Max
data C/0.0, 0.0, 0.0, 0.0, 0.0, 0.0/
data Eps1/1.E-6/, Eps2/1.E-6/, Eps3/1.E-6/, Eta/0.1/, Max/100/
integer:: Count=0
integer i
! Body of TestZR30
call ZR30(Fun, C, Eps1, Eps2, Eps3, Eta, Max, Cnt)
print *, 'The result of the program:'
print 10, (i, C(i), Cnt(i), i=1,n)
print 20, Count
10 format('Root ',I1,': ',E15.7,3X,'Num.iterations =',I3)
20 format(/' Count =',I3)
contains
real function Fun(x)
real, intent(in):: x
Fun=(x-3.0)*(x-3.01)*(x-7.0)*(x-7.0)*(x+9.0)*(x+13.0)
Count=Count+1
return
end function Fun
end program TestZR30
The result of the program:
Root 1: 0.3010000E+01 Num.iterations = 16
Root 2: 0.3000000E+01 Num.iterations = 7
Root 3: 0.6999999E+01 Num.iterations = 14
Root 4: -0.9000000E+01 Num.iterations = 9
Root 5: 0.7000000E+01 Num.iterations = 5
Root 6: -0.1300000E+02 Num.iterations = 5
Count = 59
ZR40
Программа ZR40 вычисляет все корни z[1:n] полинома p(x) = a[0]*xn + ... + a[n-1]*x + a[n] степени n методом Ньютона-Миели. Полином задаётся массивом коэффициентов a[i] (i=0, 1,...,n), где a[n] - свободный член. Полином p(x) должен иметь только вещественные корни, причём все различные (не кратные). Приближения для каждого корня уточняются путём итерации, пока для двух последовательных приближений x0 и x1 не начнёт выполняться соотношение |x1-x0| ≤ eps*|x1|. При выводе корни z[i] будут упорядочены по их величинам: z[1]>z[2]>...>z[n].
[Б10]. Алгоритм 105б
Вызов программы
call ZR40(A, N, Eps, Z)
Параметры программы
A, N, Eps - входные параметры;
Integer N - степень полинома;
Real A[0:N] - коэффициенты полинома;
Real Eps - погрешность вычисления корней;
Real Z[1:N] - массив, в который помещаются найденные корни.
Пример
!Поиск вещественных корней полинома
program TestZR40
use NML
implicit none
! Variables
integer, parameter:: N=5
real A(0:N), Z(N), Eps
data A /1.0, -28.0, 74.0, 28.0, -75.0, 0.0/
data Eps /1.0E-6/
integer i
! Body of TestZR40
call ZR40(A, N, Eps, Z)
print *, 'The result of the program:'
print 20, (i, Z(i), i=1, N)
20 format('z',I1,' = ',F10.6)
end program TestZR40
The result of the program:
z1 = 25.000000
z2 = 3.000000
z3 = 1.000000
z4 = 0.000000
z5 = -1.000000
ZR44
Программа ZR44 использует корректурные формулы Брестоу и Ньютона для нахождения всех вещественных и комплексных корней полинома. Полином p(x) = a[0]*xn + ... + a[n-1]*x + a[n] задаётся массивом коэффициентов a[i] (i=0, 1,...,n), где a[n] - свободный член. В итерационном процессе коэффициенты полинома преобразуются делением их на среднее арифметическое, вычисляемое на каждом шаге. Метод итераций Брестоу-Ньютона почти всегда сходится с точностью до k-ой цифры либо к значению корня, либо к его обратному значению. Если совместные итерации по Ньютону и Брестоу не дают сходимости за it повторений, то требование к сходимости последовательно снижается на одну значащую цифру. Для каждого корня формируется параметр acc, который информирует о ходе итерационного процесса.
[Б8]. Алгоритм 30б
Вызов программы
call ZR44(A, N, it, k, U, V, Acc)
Параметры программы
A, N, it, k - входные параметры;
Integer N - степень полинома;
Real A[0:N] - коэффициенты полинома;
Integer it - максимальное количество итераций;
Integer k - желательное количество правильных значащих цифр;
Real U[1:N] - массив, содержащий вещественные части найденных корней;
Real V[1:N] - массив, содержащий мнимые части найденных корней;
Real Acc[1:N] - массив параметров, которые используются для проверки сходимости.
Пример
! Поиск вещественных и комплексных корней полинома
program TestZR44
use NML
implicit none
! Variables
integer, parameter:: N=5
real A(0:N), U(N), V(N), Acc(N)
integer it, k
data A /1.0, 1.0, -8.0, -16.0, 7.0, 15.0/
data it /100/, k /4/
integer i
! Body of TestZR44
call ZR44(A, N, it, k, U, V, Acc)
print *, 'The result of the program:'
print 20, (i, U(i), V(i), Acc(i), i=1, N)
20 format('z',I1,' = ',F10.6,' +i',F10.6,2X,'acc=',E13.6)
end program TestZR44
The result of the program:
z1 = 3.000057 +i 0.000000 acc= 0.100000E+05
z2 = -2.000029 +i -1.000046 acc= 0.100000E+05
z3 = -2.000029 +i 1.000046 acc= 0.100000E+05
z4 = -1.000000 +i 0.000000 acc= 0.100000E+05
z5 = 1.000000 +i 0.000000 acc= 0.100000E+05
!То же, для k=5
The result of the program:
z1 = 3.000000 +i 0.000000 acc= 0.100000E+06
z2 = -2.000000 +i -1.000000 acc= 0.100000E+06
z3 = -2.000000 +i 1.000000 acc= 0.100000E+06
z4 = -1.000000 +i 0.000000 acc= 0.100000E+06
z5 = 1.000000 +i 0.000000 acc= 0.100000E+06
